[비선형 자료구조] 그래프

그래프(Graph)

• 그래프는 트리의 상위 개념의 자료구조로, 정점과 간선으로 구성된다.
• 연결된 정점간의 관계를 표현할 수 있는 자료구조이다.
• 그래프의 용도는 지하철 노선도나 통신 네트워크같은데에서 쓰인다.

그래프에서 사용되는 용어

Undirected Graph(좌), Directed Graph(우)

• 정점(Vertex) : 그래프 구조의 자료 값을 담고 있는 단위(노드)
• 간선(Edge) : 노드 간의 연결선(link, branch)
• 인접 정점(Adjacent vertex) : 간선 하나를 두고 바로 연결된 정점
• 정점의 차수(Degree) : 무방향 그래프에서 하나의 정점에 인접한 정점의 수
  • 무방향 그래프 모든 정점 차수의 합 = 그래프 간선의 수의 2배
• 진입 차수(In-degree) : 방향 그래프에서 외부에서 오는 간선의 수
• 진출 차수(Out-degree) : 방향 그래프에서 외부로 나가는 간선의 수
• 경로 길이(Path length) : 경로를 구성하는데 사용된 간선의 수
• 단순 경로(Simple Path) : 경로 중에서 반복되는 정점이 없는 경우
• 사이클(Cycle) : 단순 경로의 시작 정점과 끝 정점이 동일한 경우

그래프의 특징과 트리와의 차이

	그래프	트리
개요	노드와 간선으로 이루어진 자료구조	그래프의 한 종류
방향성	방향 그래프, 무방향 그래프 모두 존재	방향 그래프만 존재
사이클	사이클 가능, 자체 간선(Self-Loop) 가능, 순환(Cyclic), 비순환(Acyclic) 그래프 모두 존재	사이클 불가능, 자체 간선 불가능, 비순환(Acylic) 그래프만 존재
모델	네트워크 모델	계층 모델
루트 노드	루트 노드 X	최상위 노드
부모-자식	부모-자식 관계 X	인접한 상하위 노드
간선 수	그래프에 따라 간선 개수 다름	N개의 노드로 구성된 트리의 간선 수는 N-1개
순회	DFS, BFS	DFS(Pre-, In-, Post-Order) / BFS(Level-Order)
경로	2개 이상의 경로 가능	두 노드 간의 경로는 1개(유일)
예시 및 종류	노선도, 지도	이진 트리, 이진 탐색 트리, 균형 트리(AVL, RB), 이진 힙(최대힙, 최소힙)

 

그래프의 종류

• 무방향 그래프(Undirected Graph) : 두 정점을 연결하는 간선에 방향이 없는 그래프.(양방향 이동 가능) 
• 방향 그래프(Directed Graph) : 두 정점을 연결하는 간선에 방향이 있는 그래프. (방향으로만 이동 가능)
• 가중치 그래프(Weighted Graph) : 두 정점을 이동할 때 가중치만큼의 비용이 드는 그래프.(이동 비용, 방향/무방향 모두 가능) 
• 완전 그래프(Complete Graph) : 모든 정점이 간선으로 연결되어 있는 그래프.(방향/무방향 모두 가능)
  • 정점이 N개일 경우, 간선 수는 N(N-1)/2이다.

• 부분 그래프(Subgraph) : 기존 그래프에서 일부 정점이나 간선을 제외하고 만든 그래프.
• 유향 비순환 그래프(DAG, Directed Acyclic Graph) : 방향 그래프에서 사이클이 없는 그래프

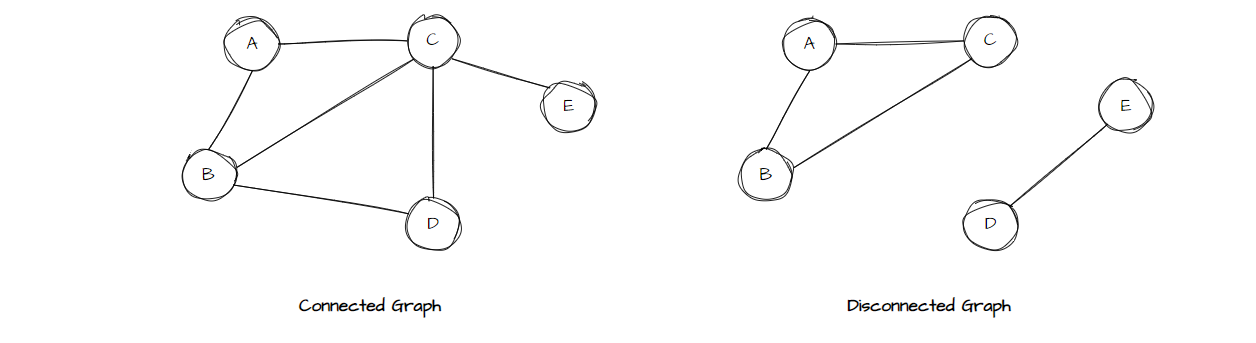
• 연결 그래프(Connected Graph) : 떨어진 정점이 없는 그래프
• 비연결 그래프(Disconnected Graph) : 떨어진 정점이 있는 그래프

그래프의 탐색(Traversal)

깊이 우선 탐색(Depth First Search = DFS)

DFS 예시

• 깊게(deep) 파고드는 형태로 탐색하는 방법이다.
• 다음 분기를 살펴보기 전에 해당 분기를 끝까지 탐색한다.
•  visited 배열과 스택으로 구현한다.
• 모든 노드를 방문 하고자 하는 경우에 이 방법을 선택 한다.

깊이 우선 탐색이 너비 우선 탐색보다 좀 더 간단하다.

너비 우선 탐색(Breath First Search = BFS)

BFS 예시

• 넓게(wide) 탐색하는 방법이다.(가까운 노드부터 순회)
• 루트 노드(시작 노드)에서 인접한 노드를 먼저 탐색하는 방법이다.
•  visited 배열과 큐로 구현한다.
• 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택한다

그래프의 구현

1. 인접 행렬(Adjacency Matrix)

인접행렬 예시

2차원 배열을 이용해서 만든다. matrix[i][j]가 0이 아니라면 i -> j 로의 간선이 존재한다는 뜻이다.

가중치 그래프가 아닌 경우에는 간선이 있으면 1, 없으면 0으로 표현하고, 가중치 그래프인 경우에는 간선이 있으면 해당 간선의 가중치, 없으면 0으로 표현한다.

무방향 그래프인 경우 대칭행렬이다.

 

인접 행렬의 장점

• 간선정보의 확인과 업데이트가 빠르다.(O(1)의 시간복잡도로 해당 간선 정보를 확인하거나 업데이트할 수 있다.)
• 정점의 차수는 O(N) 안에 알 수 있다.
• 그래프에 간선이 많이 존재하는 밀집 그래프(Dense Graph)의 경우에 유용하다.

 

인접 행렬의 단점

• 인접 행렬을 위한 메모리 공간이 추가로 필요하다.  간선의 수와 무관하게 N^2의 메모리 공간이 필요하다.
• 어떤 노드에 인접한 노드를 찾기 위해서는 모든 노드를 순회해봐야 한다.
• 그래프에 존재하는 간선의 수는 O(N^2)안에 알 수 있다. (인접 행렬 전체를 조사)

2. 인접 리스트(Adjacency List)

인접 리스트 예시

연결 리스트(인접 리스트)를 이용해서 구현하는 방법이다.

각각의 정점에 인접한 정점들을 리스트로 묶은 것이다.

무방향 그래프는 각 간선에서 두번 저장된다. ( A -> B, B -> A )

 

인접 리스트의 장점

• 장점은 메모리 사용량이 상대적으로 적고, 노드의 추가 삭제도 빠르다.
• 어떤 노드의 인접 노드를 빠르게 찾을 수 있다. 
• 그래프에 존재하는 모든 간선의 수를 O(N+E)안에 알 수 있다.(N은 정점(노드)의 수, E는 간선의 수)
• 그래프에 간선이 적게 존재하는 희소 그래프(Sparse Graph)의 경우에 유용하다.

 

인접 리스트의 단점

• 간선 정보 확인이 인접 행렬에 비해서는 상대적으로 오래 걸린다. (정점 차수(degree, 인접한 노드 수)만큼의 시간이 필요하다)

인접 행렬, 인접 리스트 복잡도 비교

	인접 행렬	인접 리스트
특정 간선 검색	O(1)	O(degree(V))
정점의 차수 계산	O(N)	O(degree(V))
전체 노드 탐색	O(N^2)	O(E)
메모리	N x N	N + E

N : 전체 정점 개수, E : 전체 간선 개수, degree : 차수

 

인접 행렬로 그래프 구현 (java)

class MyGraphMatrix {
    char[] vertices; // 정점(노드) 이름(1차원 배열)
    int[][] adjMat; // 인접 행렬(2차원 배열)
    int elemCnt;

    public MyGraphMatrix(){}
    public MyGraphMatrix(int size){
        this.vertices=new char[size];
        this.adjMat=new int[size][size];
        this.elemCnt=0;
    }

    public boolean isFull() {
        return this.elemCnt==this.vertices.length;
    }

    public void addVertex(char data){
        if(isFull()){
            System.out.println("Graph is Full!");
            return;
        }

        this.vertices[this.elemCnt++]=data;
    }

    public void addEdge(int x, int y){
        this.adjMat[x][y]=1;
        this.adjMat[y][x]=1;
    }

    public void addDirectedEdge(int x, int y){
        this.adjMat[x][y]=1;
    }

    public void deleteEdge(int x, int y){
        this.adjMat[x][y]=0;
        this.adjMat[y][x]=0;
    }

    public void deleteDirectedEdge(int x, int y){
        this.adjMat[x][y]=0;
    }

    public void dfs(int id){ // id는 시작 정점
        boolean[] visited=new boolean[this.elemCnt];
        Stack<Integer> stack=new Stack<>();

        stack.push(id);
        visited[id]=true;
        
        while(!stack.isEmpty()){
            int curId=stack.pop();
            System.out.println(this.vertices[curId]+ " ");

            for (int i = 0; i < this.elemCnt ; i++) {
                if(this.adjMat[curId][i]==1 && visited[i]==false){
                    stack.push(i);
                    visited[i]=true;
                }
            }
        }
        System.out.println();
    }

    public void bfs(int id){ // id는 시작 정점
        boolean[] visited=new boolean[this.elemCnt];
        Queue<Integer> queue=new LinkedList<>();

        queue.offer(id);
        visited[id]=true;

        while(!queue.isEmpty()){
            int curId=queue.poll();
            System.out.println(this.vertices[curId]+ " ");

            for (int i = 0; i < this.elemCnt ; i++) {
                if(this.adjMat[curId][i]==1 && visited[i]==false){
                    queue.offer(i);
                    visited[i]=true;
                }
            }
        }
        System.out.println();
    }
}

인접 리스트로 그래프 구현 (java)

class Node{
    int id;
    Node next;

    public Node(int id, Node next){
        this.id=id;
        this.next=next;
    }
}

class MyGraphList {
    char vertices[];
    Node[] adjList;
    int elemCnt;

    public MyGraphList(){}
    public MyGraphList(int size){
        this.vertices=new char[size];
        this.adjList=new Node[size];
        this.elemCnt=0;
    }

    public boolean isFull(){
        return this.elemCnt=this.vertices.length;
    }

    public addVertex(char data){
        if(isFull()){
            System.out.println("Graph is full");
            return;
        }

        this.vertices[this.elemCnt++]=data;
    }

    public void addEdge(int x, int y){
        this.adjList[x]=new Node(y, this.adjList[x]);
        this.adjList[y]=new Node(x, this.adjList[y]);
    }

    public void addDirectedEdge(int x, int y){
        this.adjList[x]=new Node(y, this.adjList[x]);
    }

    public void deleteEdge(int x, int y){
        Node cur=this.adjList[x];
        Node prev=this.adjList[x];
        while(cur.id!=y){
            prev=cur;
            cur=cur.next;
        }
        prev.next=cur.next;
        cur.next=null;

        cur=this.adjList[y];
        prev=this.adjList[y];
        while(cur.id!=x){
            prev=cur;
            cur=cur.next;
        }
        prev.next=cur.next;
        cur.next=null;
    }

    public void deleteDirectedEdge(int x, int y){
        Node cur=this.adjList[x];
        Node prev=this.adjList[x];
        while(cur.id!=y){
            prev=cur;
            cur=cur.next;
        }
        prev.next=cur.next;
        cur.next=null;
    }
    
    public void dfs(int id){
        boolean[] visited=new boolean[this.elemCnt];
        Stack<Integer> stack=new Stack();
        
        stack.push(id);
        visited[id]=true;
        
        while(!stack.isEmpty()){
            int curId=stack.pop();
            System.out.println(this.vertices[curId] + " ");
            
            Node cur=this.adjList[curId];
            while(cur!=null){
                if(visited[cur.id]==false){
                    stack.push(cur.id);
                    visited[cur.id]=true;
                }
                cur=cur.next;
            }
        }
        System.out.println();
    }
    
    public void bfs(int id){
        boolean[] visited=new boolean[this.elemCnt];
        Queue<Integer> queue=new LinkedList<>();

        queue.offer(id);
        visited[id]=true;

        while(!queue.isEmpty()){
            int curId=queue.poll();
            System.out.println(this.vertices[curId] + " ");

            Node cur=this.adjList[curId];
            while(cur!=null){
                if(visited[cur.id]==false){
                    queue.offer(cur.id);
                    visited[cur.id]=true;
                }
                cur=cur.next;
            }
        }
        System.out.println();
    }
}