[비선형 자료구조] 힙(Heap)

힙에 들어가기에 앞서, 이진 트리에 대해서는 알아두는 편이 좋다.

이진 트리 포스팅

트리(1) - 이진 트리(Binary Tree)

힙(Heap)

힙 예시

• 힙은 우선순위 큐를 구현하는데 자주 사용되는 자료구조이다. ( 우선순위 큐 링크 )
• 완전 이진 트리(Complete Binary Tree) 형태이다.(왼쪽부터 차곡히 다 쌓인 트리)
• BST(이진 탐색 트리)와 달리 중복 값을 허용한다.
• 반 정렬 상태(느슨한 정렬 상태)를 유지한다. 반 정렬 상태가 무슨 뜻이냐면
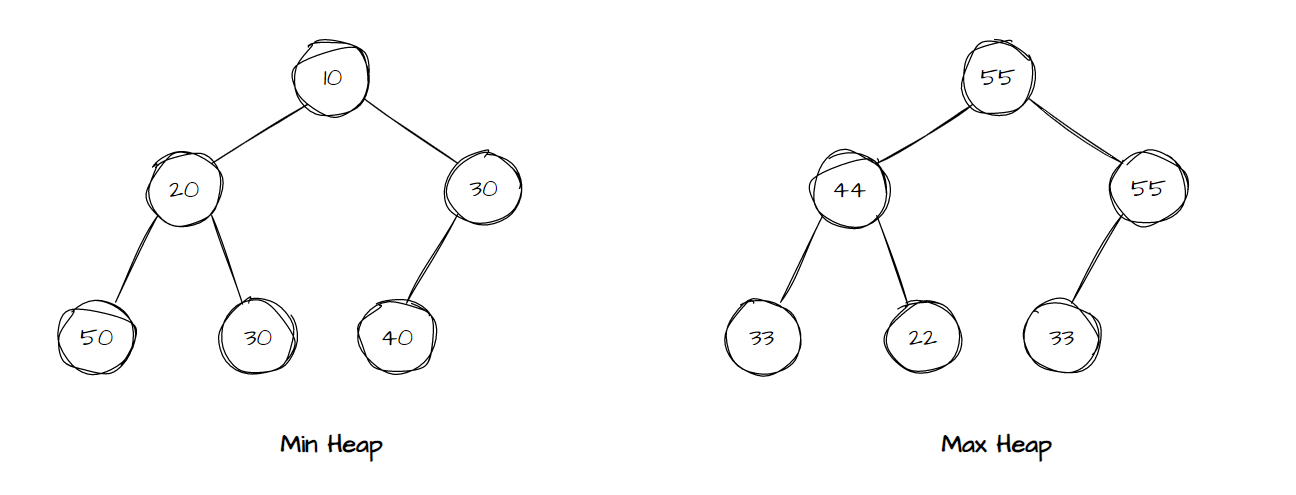
  • 최소 힙(Min Heap)에서는 루트 노드(최상단 노드)가 가장 최소값이고, 최소 힙 기준으로 부모 노드의 값은 자식 노드보다 작다.
  • 최대 힙(Max Heap)에서는 루트 노드(최상단 노드)가 가장 최대값이고, 최대 힙 기준으로 부모 노드의 값은 자식 노드보다 크다.
  • 이때 형제들간의 값의 크기에 대한 우선순위는 보장해주지 않기 때문에 반 정렬 상태라고 부른다.
• 루트 노드부터 자료를 빼내면 최대힙은 큰 순서대로, 최소는 작은 순서대로 쭉 빼낼 수 있다. 그래서 최소값이나 최댓값을 찾는데 유용한 자료구조이다.

힙의 활용 예시

• 시뮬레이션 시스템
• 네트워크 트래픽 제어
• 운영 체제에서의 작업 스케쥴링
• 수치 해석적인 계산
• 허프만 코드(힙의 구조가 기반)
• 힙 정렬
• 우선순위 큐

시간복잡도

삽입과 삭제 자체에는 O(1)이 걸리지만 삽입, 삭제로 인해 깨진 힙의 구조를 재구조화(Heapify)하는 과정까지 포함하여 O(logN)이 걸린다. 그래도 최대, 최소값 탐색은 O(1)이면 된다. (그냥 루트 노드 가져오면 되기 때문)

(즉, 삽입, 삭제 - O(logN))

힙의 종류

최소 힙(Min Heap)

최소 힙 예시

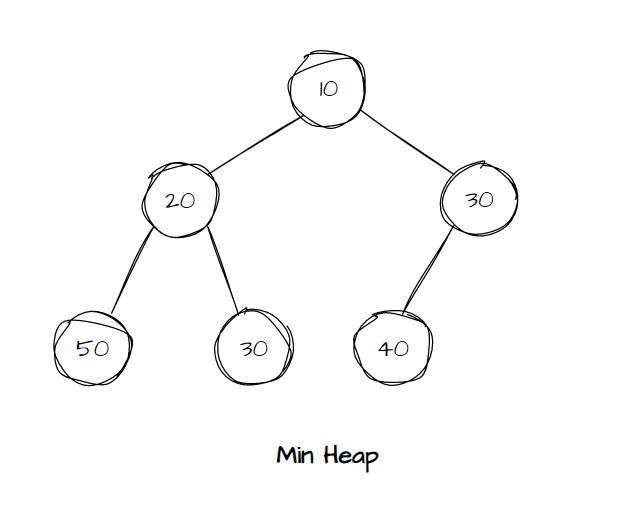
최소 힙은 부모노드의 키가 자식 노드의 키보다 작거나 같은 형태이다.

key(부모 노드) <= key(자식 노드) 라는 뜻이다.

최대 힙(Max Heap)

최대 힙 예시

최대 힙은 부모노드의 키가 자식 노드의 키보다 크거나 같은 형태이다.

key(부모 노드) >= key(자식 노드) 라는 뜻이다.

 

이제부터 설명할 힙의 삽입, 삭제는 최소 힙, 최대 힙 모두 구조가 같으므로 최소 힙을 기준으로 설명하도록 하겠다.

힙의 삽입(insert)

과정은 다음과 같다.

1. 트리의 가장 끝 위치에 데이터 삽입
2. 부모 노드와  키를 비교한 후 작을 경우, 부모 자리와 교체하며 제 자리를 찾을 때까지 반복한다.(Heapify)

힙의 삭제(delete)

과정은 다음과 같다.

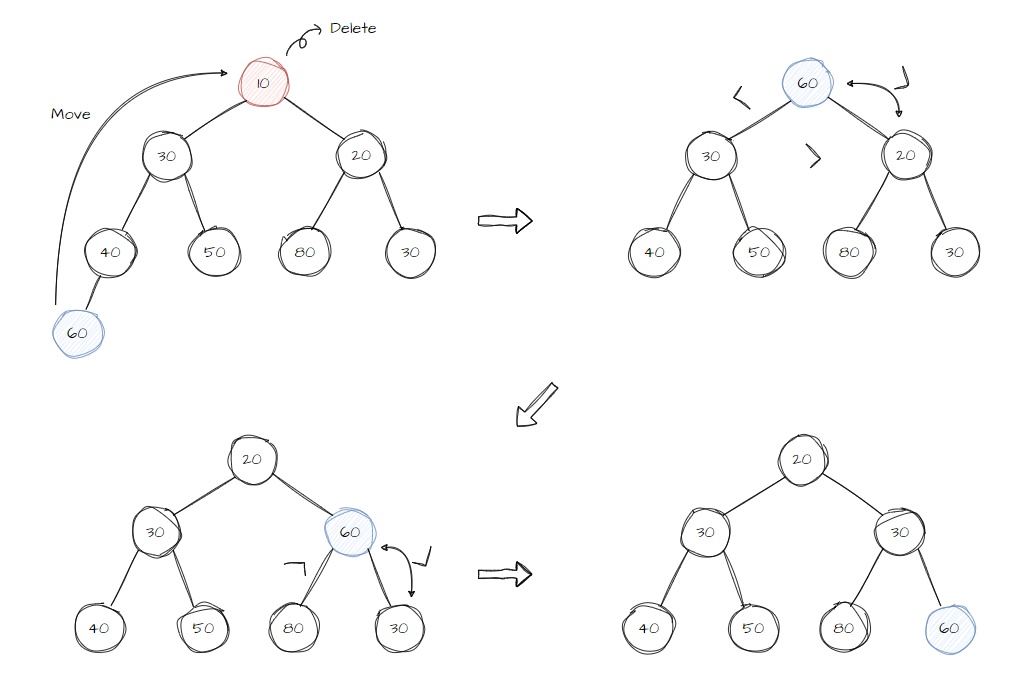
1. 최상위 노드(루트 노드)를 반환하면서 삭제한다.(pop 하듯이)
2. 가장 마지막 위치 노드를 최상위 노드로 위치시킨다.
3. 맞는 자리를 찾을때까지 교체를 반복한다.(더 작은 쪽이랑 교체한다.)(Heapify)

힙의 구현(java)

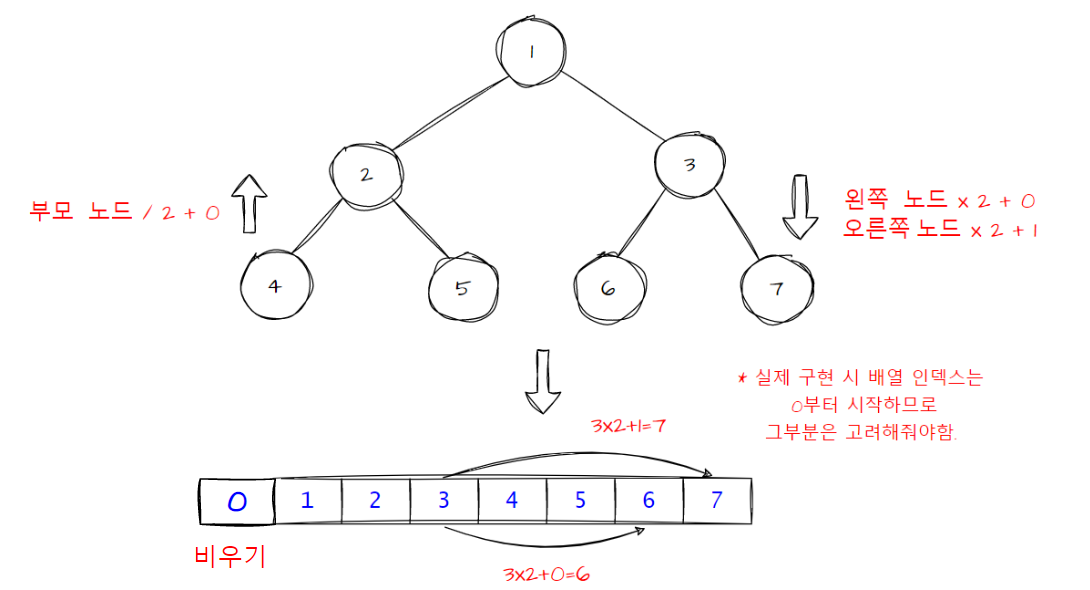
힙은 완전 이진 트리 형태가 보장되기 때문에 배열(or ArrayList)로 편하게 구현이 가능하다.

구현을 쉽게 하기 위해 0번 index는 비우고 루트 노드를 배열의 1번 index에 저장한다. 그리고 각 노드를 기점으로 왼쪽 자식노드는 a[i∗2+1], 오른쪽 자식노드는 a[i∗2+2] 의 index에 저장한다. 또한 특정 index의 노드에서 부모노드는 a[(i−1)/2]로 찾을 수 있다.

정리하자면 아래와 같다.

• 루트 노드 - a[1]
• 왼쪽 자식 노드 - a[i*2+1]
• 오른쪽 자식 노드 - a[i*2]
• 부모 노드 - a[(i-1)/2]

최소 힙 구현 코드(java)

class MinHeap{
    ArrayList<Integer> heap;

    public MinHeap() {
        this.heap = new ArrayList<>();
        this.heap.add(0);
    }

    public void insert(int data) { 
        heap.add(data); // 가장 끝 위치에 데이터 추가

        // 추가한 후 부모와 크기 비교하며 자기 자리 찾아가기
        int cur = heap.size() - 1;
        while (cur > 1 && heap.get(cur / 2) > heap.get(cur)) {
            int parentVal = heap.get(cur / 2);
            heap.set(cur / 2, data);
            heap.set(cur, parentVal);

            cur /= 2;
        }
    }

    public Integer delete() {
        if (heap.size() == 1) {
            System.out.println("Heap is empty!");
            return null;
        }
        
        // delete 대상 노드는 가장 상위 노드
        int target = heap.get(1);
        
        // 마지막 노드를 가장 위로 설정 후 마지막 노드는 삭제
        heap.set(1, heap.get(heap.size() - 1));
        heap.remove(heap.size() - 1);

        int cur = 1;
        while (true) {
            int leftIdx = cur * 2;
            int rightIdx = cur * 2 + 1;
            int targetIdx = -1;

            if (rightIdx < heap.size()) { // 자식 노드 둘다 있는 경우
                targetIdx = heap.get(leftIdx) < heap.get(rightIdx) ? leftIdx : rightIdx;
            } else if (leftIdx < heap.size()) { // 왼쪽 자식 노드만 있는 경우
                targetIdx = cur * 2;
            } else {
                break;
            }

            if (heap.get(cur) < heap.get(targetIdx)) {  // 부모가 작으면 종료
                break;
            } else {    // 부모가 더 크면 자리 바꾸기
                int parentVal = heap.get(cur);
                heap.set(cur, heap.get(targetIdx));
                heap.set(targetIdx, parentVal);
                cur = targetIdx;
            }
        }

        return target;
    }
}

최대 힙 구현 코드(java)

class MaxHeap{
    ArrayList<Integer> heap;

    public MaxHeap() {
        this.heap = new ArrayList<>();
        this.heap.add(0);
    }

    public void insert(int data) {
        heap.add(data);

        int cur = heap.size() - 1;
        while (cur > 1 && heap.get(cur / 2) < heap.get(cur)) {
            int parentVal = heap.get(cur / 2);
            heap.set(cur / 2, data);
            heap.set(cur, parentVal);

            cur /= 2;
        }
    }

    public Integer delete() {
        if (heap.size() == 1) {
            System.out.println("Heap is empty!");
            return null;
        }

        int target = heap.get(1);

        heap.set(1, heap.get(heap.size() - 1));
        heap.remove(heap.size() - 1);

        int cur = 1;
        while (true) {
            int leftIdx = cur * 2;
            int rightIdx = cur * 2 + 1;
            int targetIdx = -1;

            if (rightIdx < heap.size()) {
                targetIdx = heap.get(leftIdx) > heap.get(rightIdx) ? leftIdx : rightIdx;
            } else if (leftIdx < heap.size()) {
                targetIdx = cur * 2;
            } else {
                break;
            }

            if (heap.get(cur) > heap.get(targetIdx)) {
                break;
            } else {
                int parentVal = heap.get(cur);
                heap.set(cur, heap.get(targetIdx));
                heap.set(targetIdx, parentVal);
                cur = targetIdx;
            }
        }

        return target;
    }
}