[비선형 자료구조] 트리(2) - 이진탐색트리

저번 포스팅에선 트리, 이진 트리에 대해 알아보았다.

[비선형 자료구조] 트리 링크

트리(1) - 이진 트리(Binary Tree)

트리(3) - AVL 트리

트리(4) - Red-Black 트리

 

이번 포스팅에서는 이진 탐색 트리에 대해 알아보자.

이진 탐색 트리(Binary Search Tree = BST)

이진 탐색 트리는 이진 트리의 종류중 하나로 다음과 같은 특징을 가지고 있다.

1. 왼쪽 자식 노드의 키는 부모 노드의 키보다 작다.
2. 오른쪽 자식 노드의 키는 부모 노드의 키보다 크다.
3. 각각의 서브트리도 이진탐색트리를 유지한다.
4. 중복된 키를 허용하지 않는다.

균형상태(좌), 불균형상태(우)

중위순회(왼중오)하면 오름차순으로 (탐색)나온다. 기존 이진트리에 비해 탐색이 빠르다.(하지만 균형 유지가 필요하다.)

이진 트리는 규칙없이 데이터가 들어가있다보니까 어떤걸 탐색할 때는 모든 데이터를 worst case로 탐색해봐야 했지만 이진 탐색 트리는 균형상태일 경우 부모에서 큰지 작은지만 결정하면 한 방향이 결정되기 때문에 O(logN)으로 탐색이 가능하다. 불균형 상태일 경우 결국 모든 노드를 탐색하여 O(N)의 탐색이 되기 때문에 이부분은 생각해줘야 한다.

* 균형은 모든 노드의 좌우 서브 트리 높이가 1이상 차이나지 않는 트리를 말한다.

 

이진 탐색 트리에서의 탐색

이진 탐색 트리 탐색 예시(24 탐색)

• 찾고자 하는 데이터를 루트 노드부터 비교하기 시작한다.
• 대소비교를 하여 데이터가 작으면 왼쪽, 크면 오른쪽으로 간다.
• 찾는 데이터가 없으면 null을 반환한다.
• 어떤 데이터를 찾더라도 최대 트리 높이만큼만 탐색이 이루어진다.

삽입

이진 탐색 트리 삽입 예시

1. 루트노드부터 비교하기 시작한다.(중복 키 발견시 노드 추가하지 않고 종료)
2. 삽입할 키가 현재 노드의 키보다 작으면 왼쪽, 크면 오른쪽으로 이동한다.
3. Leaf에 도달 후 키를 비교하여 작으면 왼쪽, 크면 오른쪽으로 간다.

삭제

먼저 탐색해서 삭제 대상 노드를 찾는다.

삭제 대상 노드가 가진 자식노드의 수에 따라 방법이 조금씩 달라진다.

삭제 대상 노드가 Leaf 노드일 경우

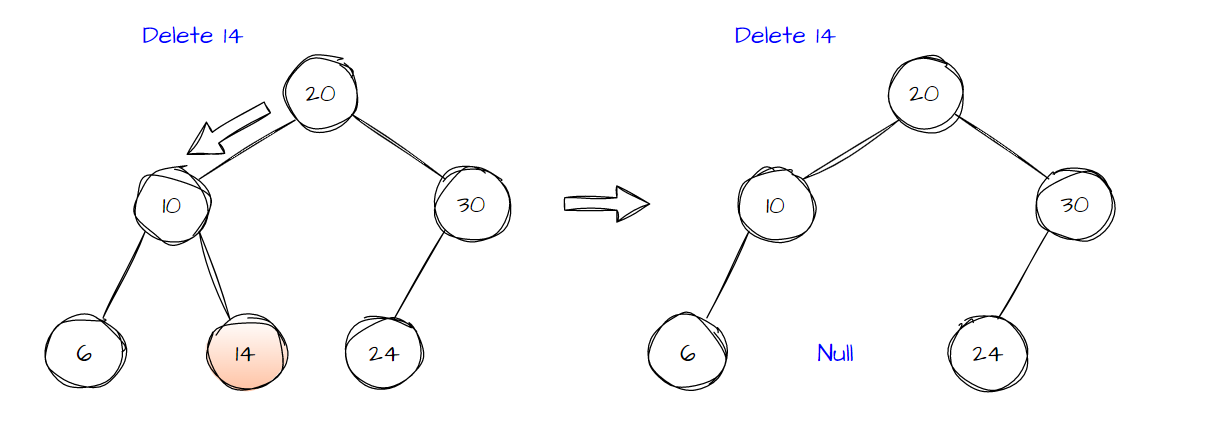
i)  삭제 대상 노드가 Leaf 노드인 경우, 삭제 대상 노드 삭제, 부모 노드의 해당 자식 링크 null로 변경한다.

삭제 대상 노드가 자식 노드를 하나 가질 경우

ii) 삭제 대상 노드가 자식 노드가 하나 있는 경우, 삭제대상노드의 부모노드와 삭제대상노드의 자식노드를 연결해준다.

삭제 노드가 자식 노드를 둘 가질 경우(1번 방법)

iii) 삭제 대상 노드가 자식 노드가 둘 있는 경우 2가지 방법이 있다.

1. 삭제 대상 노드의 왼쪽 서브 트리에서 가장 큰 노드를 선택하고, 삭제 대상 노드 위치에 그걸 올린다. 그리고 삭제 대상 노드 삭제한다.(선택한 가장 큰 노드가 왼쪽 자식을 가질경우, 자식 노드는 선택 노드의 부모 노드에 연결해준다.)
2. 삭제 대상 노드의 오른쪽 서브 트리에서 가장 작은 노드를 선택하고, 삭제 대상 노드 위치에 그걸 올린다. 그리고 삭제 대상 노드 삭제한다.(선택한 가장 작은 노드가 오른쪽 자식을 가질경우, 자식 노드는 선택 노드의 부모 노드에 연결해준다.)

BST구현 (java)

import java.util.LinkedList;
import java.util.Queue;

class BinarySearchTree {
    Node head;

    BinarySearchTree(int key) {
        this.head = new Node(key, null, null);
    }

    public Node addNodeRecursive(Node cur, int key) {
        if (cur == null) {
            return new Node(key, null, null);
        }

        if (key < cur.key) {
            cur.left = addNodeRecursive(cur.left, key);
        } else {
            cur.right = addNodeRecursive(cur.right, key);
        }

        return cur;
    }

    public Node removeNodeRecursive(Node cur, int key) {
        if (cur == null) {
            return null;
        }

        if (key < cur.key) {
            cur.left = removeNodeRecursive(cur.left, key);
        } else if (key > cur.key) {
            cur.right = removeNodeRecursive(cur.right, key);
        } else {
            if (cur.left == null) { // 왼쪽 자식노드가 하나 혹은 없는 경우
                return cur.right;
            } else if (cur.right == null) { // 오른쪽 자식노드가 하나 혹은 없는 경우
                return cur.left;
            } else { // 자식노드가 둘인 경우
                Node predecessor = cur; // 선택노드의 부모노드
                Node successor = cur.left; // 선택노드

                while (successor.right != null) {
                    predecessor = successor;
                    successor = successor.right;
                }

                predecessor.right = successor.left;
                cur.key = successor.key;
            }
        }

        return cur;
    }

현재까지 구현한 기본적인 이진 탐색 트리의 경우 삽입 순서에 따라 편향이 발생할 수 있다.

다음 포스팅에서는 BST의 종류중 조건에 맞춰 균형을 유지하도록 하는 AVL 트리, Red-Black 트리에 대해 알아보도록 하자.