학교에서 분명 배웠던 것 같은데, 수열과 순열은 항상 헷갈리고, 조합 계산식도 기억이 안난다.
그럼 정리해보자.
수열(Sequence)
수열 a이란 정의역이 순서수(ordinal number) α ∈ ON인 함수를 말한다.
a:α→S
뭐라는지 모르겠는가? 필자도 그렇다. 쉽게 다가가보자. 쉽게 말하자면 수열은 어떤 규칙에 따라서 숫자들을 늘어놓은걸 말한다. (규칙이 없어도 수열이라고는 하지만 그건 몰라도 된다.)
수열은 일반적으로
등차수열
연속된 두 항의 차이가 일정한 수열( ex - 2,4,6,8,10,12...)



등차수열 일반항과 등차수열의 합 공식이다. 굳이 외울 필요는 없지만 알아둔다면 가끔 반복문을 한두개 지우는데 도움이 될 수도 있으니 알아두는 것이 좋다.
등비수열
연속된 두 항의 비가 일정한 수열( ex - 2,6,18,54...(공비=3))


마찬가지로 반복문을 한두개 지우는데 도움이 될 수 있으므로 알아두자.
계차수열

어떤 수열의 인접하는 두 항의 차로 이루어진 또 다른 수열이다.
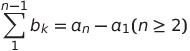
수열 {an}의 계차수열이 {bn}이라고 할 때 위와 같은 식을 만족한다.
피보나치 수열

세번째 항은 두번째 항과 첫번째 항을 더한 합인 수열
순열(Permutation)
그럼 순열은 무엇일까. 서로 다른 개의 원소에서 개를 중복없이 순서에 상관있게 선택하는 혹은 나열하는 것을 순열이라고 한다.

이런 느낌이다. ,
5명을 3줄로 세우는 방법, 서로다른 4명 중 반장, 부반장을 뽑는 방법 등의 문제를 풀 때 쓰인다.
잘 감이 안온다면 직접 수를 대입해서 생각해보면 편하다. 예를 들어, ₅P₃ = 5! / (5 - 3)! = 5 * 4 * 3 = 60이다.
문제로 예를 들어 보자면 { 1, 2, 3, 4 } 에서 3개를 뽑아 나열하는 법을 찾아보면 { 1, 2, 3 }, { 1, 2, 4 } ... { 2, 3, 4 } 이런식으로 첫번째에 뭘 뽑는지에 따라 순서가 달라진다. 그래서 ₄P₃ = 4 * 3 * 2 = 24가지가 나온다.
(n - r + 1)같은거는 알아두는게 좋다. 실제 순열을 반복문을 통해 구현할 때 얼만큼 반복을 해야하는지를 알 수 있다.
순열에도 여러가지 종류가 있다. 몇개정도 알아보자.
팩토리얼(계승, Factorial - n!)
기호로 간단하게 n!이며, 1부터 n까지의 자연수를 모두 곱하는 걸 의미한다.(0!=1이다.)
중복순열(product)

서로 다른 n개 중에 r개를 선택하는 경우의 수인데, 이 경우 순서가 있고, 중복을 허용한다.
서로 다른 4개의 수 중 2개를 뽑는 방법, 후보 2명, 유권자 3명일 때 기명 투표 방법 등의 문제를 풀 때 쓰인다.
원순열(norm of cyclic group)

원 모양의 테이블에 n개의 원소를 나열하는 경우의 수이다.
원 모양의 테이블에 3명을 앉히는 경우 등의 문제를 풀 때 쓰인다. 위 순열의 예제를 그대로 보면 { 1, 2, 3 }과 { 2, 3, 1 }을 원형 테이블에 앉혀두면 같은 결과이므로 이런 결과값을 세지 않는다는 의미이다.
순열구현(Java)
// 순열
for (int i = n; i >= n - r + 1; i--) {
result *= i;
}
System.out.println("result = " + result);
// 중복 순열
for (int i = 0; i < r; i++) {
result *= n;
}
// 원 순열
for (int i = 1; i < n; i++) {
result *= i;
}예제로 1, 2, 3, 4중 세개를 뽑아 나열하는 문제를 한번 풀어보자.
public class Main {
void permutation(int[] arr, int depth, int n, int r, boolean[] visited, int[] out) {
if (depth == r) {
System.out.println(Arrays.toString(out));
return;
}
for (int i = 0; i < n; i++) {
if (visited[i] != true) {
visited[i] = true;
out[depth] = arr[i];
permutation(arr, depth + 1, n, r, visited, out);
visited[i] = false;
}
}
}
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4};
boolean[] visited = new boolean[4];
int[] out = new int[3];
Main a = new Main();
a.permutation(arr, 0, 4, 3, visited, out);
}
}
재귀함수로 풀었다. permutation함수는 permutation(배열, 자릿수, n, r, visited, 결과를 담는 배열)을 인자로 받는다. visited는 해당 숫자를 방문, 뽑았는지 아닌지를 기록하는 배열이다.
out에는 {1,2,3,4}가 들어갈 세 자리가 마련되어 있고, depth는 몇번 자리인지를 말한다. depth가 0이면 out의 첫번째 자리를 의미하고, 1이면 두번째 자리를 의미하는 것이다.
depth == r 이면 모든 자리에 숫자가 들어갔다는 것을 의미하므로 out을 한번 출력해주고, return 된다.
return 되면 visited[i]를 false로 만들어 자리를 비워주고 다른 숫자가 들어가도록 하면서 모든 경우의 수를 출력하는 것이다.
디버깅하거나 그리면서 생각해보면 이해가 쉽게 갈 것이다.
순열(Python)
파이썬의 itertools를 이용하면 순열을 간단하게 만들 수 있다.
사용 전에 주의사항 : combinations, permutations, product 세 메소드 모두 generator이기 때문에 list()로 캐스팅하여 다른 곳에 저장 해두지 않으면 한 번의 루핑 이후 사라진다고 한다.
import itertools
arr = ['A', 'B', 'C']
#순열
nPr = itertools.permutations(arr, 2) # permutations(반복가능한 객체, r)
print(list(nPr))
# [('A', 'B'), ('A', 'C'), ('B', 'A'), ('B', 'C'), ('C', 'A'), ('C', 'B')]
# 각 요소는 tuple이다. for문으로 각 요소 접근가능.(수정은 불가능)조합(Combination)
조합은 서로 다른 n개의 원소에서 r개를 중복도 없고 순서도 상관없게 선택하는 경우의 수이다. 순열과 다른 부분은 어떤 순서로 원소를 선택했는지는 중요하지 않다는 점이다.


서로 다른 4명 중 주번 2명을 뽑는 경우 등의 문제를 풀 때 쓰인다.
코드로 구현할 땐 위에서 구한 순열에 r!을 나눠주면 된다.
순열 예시 문제로 예를 들어 보자면 { 1, 2, 3, 4 } 에서 3개를 뽑는 법을 찾아보면 { 1, 2, 3 }, { 1, 2, 4 } ... { 2, 3, 4 } 이런식으로 나오는데 조합은 {1,2,3}이던 {3,2,1}이던 순서를 신경쓰지 않기 때문에 이런 경우를 제외시켜줘야 한다.
그래서 ₄C₃ = ₄P₃ / 3! = 24/6 = 4가지가 나온다.
중복조합(multiset coefficient)

서로 다른 n개 중에서 r개를 선택하는 경우의 수이다. 순서는 없고 중복은 허용한다.
후보 2명, 유권자 3명일 때 무기명 투표하는 방법 등의 문제를 풀 때 쓰인다. 코드로 구현할 땐 따로 구현하지 않고, 조합으로 변환해서 구해주면 된다.
조합구현(Java)
// 조합
int combination(int n, int r) {
int pResult = 1;
for (int i = n; i >= n - r + 1; i--) { // 순열
pResult *= i;
}
int fResult = 1;
for (int i = 1; i <= r; i++) { // r!
fResult *= i;
}
return pResult / fResult;
}조합(Python)
파이썬의 itertools를 이용하면 조합을 간단하게 만들 수 있다.
import itertools
arr = ['A', 'B', 'C']
#조합
nCr = itertools.combinations(arr, 2)
print(list(nCr))
#중복조합
for cwr in combinations_with_replacement([1,2,3,4], 2):
print(cwr, end=" ")
